飞盘运动模型的物理学

飞盘的物理学

摘要

飞盘是常见的娱乐方式和运动，虽然这些飞盘背后的物理常常被视为是理所当然。飞盘的运转主要基于两个主要物理概念，空气动力学升降和**陀螺稳定性(陀螺仪惯性)**。当飞盘在空中飞行时，可以被看作是一个翼，通过伯努利原理来控制提升力的大小，使飞盘悬浮在空中。 施加的各种力不在盘的中心，因此需要防止飞盘在高角动量上翻转。该角动量抑制由各种力引起的扭矩。 编写了使用欧拉方法的计算机程序来模拟飞盘飞行的轨迹。用不同的攻角和不同的距离和高度观察到飞盘达到不同位置的试验。

介绍

几十年来，飞盘已经成为所有年龄段人们广泛使用的娱乐源。他们创造了许多新的运动（终极飞盘，高尔夫球和其他），飞盘每年的销售量比棒球，篮球和足球加起来还多。这些简单的塑料飞盘可以飞行很长的距离，似乎飞盘悬停在空中时能抵抗重力。大多数人认为飞盘背后的物理是理所当然的，但飞盘的运动模型一般可以只使用气动升降和陀螺稳定性两个物理概念来解释。现代飞盘的历史可以追溯到1871年William Russell Frisbie在Bridgeportd的Connecticut开了一个名叫The Frisbie Pie的小面包公司。Frisbie的馅饼在附近的耶鲁大学很受欢迎，学生们开始享受折腾空的饼罐。这开始变得受欢迎，学生开始称罐子为“Frisbies”和抛罐子的行为叫“Frisbieing”。第一次生产实际的塑料飞盘是在1958年Fred Morrison买了“飞盘”的专利后，但直到1958年当Wham-O发布了他们的商标“飞盘”时才真正流行起来。最近，Hummel已经对飞盘进行了研究以确定作用在飞盘上的所有力的大小以及涉及投掷飞盘的生物力学的系数Hummel（2003）。此外，还有一个未发表的研究，研究飞盘的其他方面，包含直接从飞盘飞行获取数据的方法。

飞盘飞行理论

飞盘包含的两个主要物理概念是空气动力学升降（或伯努利原理）和陀螺稳定性。旋转飞盘可以被看作是自由飞行中的机翼，伯努利原理是提供升力的原因，并且飞盘的角动量提供其稳定性。

空气动力

作用在飞盘上的两个主要空气动力是阻力和升力。为了确定这些力的大小，将使用两种非常常见的物理关系来描述。为了计算阻力，我们首先必须找到系统的雷诺数，以便知道应用哪个阻力关系。雷诺数R由下式给出：
$$ \mathbf{R} = \mathbf{\frac{ρvd}{η}} \tag1 $$

  • ρ 表示流体的密度(对于飞盘，流体即空气)
    (海平面，空气的密度约等于$1.23 kg/m^3$)
  • v 表示飞盘与流体(空气)的相对速度
  • d 表示物体的特征尺寸（对于飞盘，特征尺寸是它的直径）
  • η 表示流体(空气)的粘稠度
    通常取$η=1.73×10^−5 Ns/m^2$

对于这个量级的雷诺数，将使用Prandtl关系来计算阻力$F_d$，并且由下式给出:
$$ \mathbf{F}_{d} = \mathbf{\frac{-\mathbf{C_{D}}ρπ r^2v^2}{2}} = \mathbf{\frac{-\mathbf{C_{D}}ρπ Av^2}{2}} \tag2 $$
系数$C_{D}$是随物体变化的阻力系数，并且在Hummel（2003）中给出为仅取决于攻角α的二次函数。攻角α是飞盘平面和相对速度矢量之间的夹角。
$$ \mathbf{C_{D}} = \mathbf{C_{D0}}+\mathbf{C_{Dα}}(\mathbf{α}-\mathbf{α_{0}}) \tag3$$
系数$C_{D0}$，$α_{0}$和$C_{Dα}$是常数并且取决于飞盘本身。
飞盘受到的升力与飞机机翼上的升力非常相似，并且使用伯努利原理计算。伯努利原理众所周知，它表明流体在同一流线上的任何点的速度，压力和高度之间存在着关系。流体以快速流动的那一侧压力比慢速流动的那一侧压力更低。公式:
$$ \frac{\mathbf{v^2_{1}}}{2} + \frac{\mathbf{p}{1}}{ρ} + \mathbf{g}\mathbf{h{1}} = \frac{\mathbf{v^2_{2}}}{2} + \frac{\mathbf{p_{2}}}{ρ} + \mathbf{g}\mathbf{h_{2}} \tag4 $$

  • v 流体速度
  • p 流体压力
  • ρ 流体密度
  • g 重力加速度
  • h 流体高度

下标1和2指沿着相同流线的流体中的不同点。这个方程通常被称为伯努利方程。在上方流动的空气和在飞盘下方流动的空气之间的高度差是可忽略的，因此两个高度相关项抵消。我们还假定飞盘上面流动的空气的速度与飞盘下面的空气的速度成正比，因为路径长度的差是恒定的(i.e. $v_{1}=C_{v_{2}}$),等式如下:
$$ \frac{\mathbf{C^2v^2_{2}}}{2} + \frac{\mathbf{p_{1}}}{ρ} = \frac{\mathbf{v^2_{2}}}{2} + \frac{\mathbf{p_{2}}}{ρ} \tag5 $$

设置$F_{L}/A=p_{1}-p_{2}，F_{L}-升力，A-飞盘面积,F_{L}$等式:
$$ \mathbf{F_{L}}=\frac{1}{2}\mathbf{ρ}\mathbf{v^2A}\mathbf{C_{L}} \tag6 $$
在确定（6）所需的整个步骤中，系数C是并入系数C_{L}。C_{L}是Hummel（2003）给出的攻角α的线性函数。$$ \mathbf{C_{L}}=\mathbf{C_{L0}}+\mathbf{C_{Lα}}\mathbf{α} \tag7 $$

$C_{L0}$和$C_{Lα}$是取决于飞盘物理特性的常数。

陀螺稳定性

人们发现趣飞盘的旋转是飞盘飞行的机制中的必要组成部分，没有旋转，飞盘只会像落叶一样飘向地面，不能产生长距离，稳定的飞行。 这是由于前面部分中描述的空气动力不直接集中在飞盘上的事实造成的。一般来说，盘前半部的升力稍大于后半部的升力，这会在飞盘上产生扭矩（见图1）。
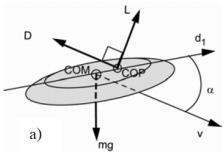
frisbee
图1.偏心中心压力（COP）和质心（COM）导致施加在飞盘上的扭矩
当飞盘不旋转时，这个小扭矩会使飞盘前半部分翻转，会使飞盘稳定性降低。当飞盘高速旋转抛出的，那么它有较大角动量，使其具有在正或负垂直方向上的向量。当施加小扭矩时，扭矩矢量指向右侧侧面（当从后面观察时）。这可以使用righthad规则：
$$ \vec{\tau}=\vec{r}×\vec{F} \tag8 $$
来源于:
$$ \vec{\tau} = \frac{d\vec{L}}{dt} \tag{9}$$
角动量向量将开始向右驱动，即投掷飞盘时飞盘会靠右或者靠左飞行，正是这个原因。因此，给予飞盘的初始角动量越大，它的飞行会更稳定。

飞盘飞行的数值建模

为了模拟飞盘的飞行，编写了一个C++程序，该程序使用了应用于上一节中所描述的力的数值技术欧拉法（参见附录中的代码）。 为了实现这一点，不同的力被分成水平和垂直分量，并且每个分量应用欧拉方法。应当注意，在该模型中，假设飞盘被给予足够的初始旋转，以便保持稳定的飞行。 在应用欧拉方法中，飞盘的轨迹被分成离散的时间步长Δt，并且在每个步骤处新的水平速度v和水平位置x，定义:
$$ \mathbf{v_{i+1}} = \mathbf{v_{i}} + \mathbf{Δv} \tag{10} $$
$$ \mathbf{x}_{i+1} = \mathbf{x}_{i} + \mathbf{Δx} \tag{11}$$
其中Δv和Δx分别是速度和位置的变化。与方程（11）类似的方程可以与垂直方向一起使用位置y，而不是x。
通过求解得到Δv以下关系:
$$ \mathbf{F_{x}} = \mathbf{F_{D}} \tag{12}$$
$$ \mathbf{m}\frac{Δ\mathbf{v_{x}}}{Δt} = \frac{1}{2}\mathbf{ρ}{\mathbf{v_{x}}}^2\mathbf{A}\mathbf{C_{D} }\tag{13} $$
$$ \mathbf{Δv_{x}} = \frac{1}{2m}\mathbf{ρ}{\mathbf{v_{x}}}^2\mathbf{A}\mathbf{C_{D}}\mathbf{Δt} \tag{14} $$
其中F_{D}是阻力,那么:
$$ \mathbf{F_{y}} = \mathbf{F_{g}} + \mathbf{F_{l}} \tag{15}$$
$$ \mathbf{m}\frac{Δ\mathbf{v_{x}}}{Δt} = \mathbf{mg}\frac{1}{2}\mathbf{ρ}{\mathbf{v_{x}}}^2\mathbf{A}\mathbf{C_{D}} \tag{16}$$
$$ \mathbf{Δv_{y}} = (g+\frac{1}{2m}\mathbf{ρ}{\mathbf{v_{x}}}^2\mathbf{A}\mathbf{C_{L}})Δt \tag{17}$$
其中下标x和y分别表示水平速度和垂直速度，F_{g}是重力。
Δx和Δy，如

$$ \mathbf{Δx}=\mathbf{v_{x}}\mathbf{Δt} \tag{18} $$
$$ \mathbf{Δy}=\mathbf{v_{y}}\mathbf{Δt} \tag{19} $$

写的程序包含一个模拟方法，需要五个输入参数，初始y(垂直)位置，初始y速度，初始x速度（初始x位置始终设置为零），攻角（以度为单位）和Δt。 除攻角以外的所有单位均为SI单位。在所有试验中，使用Δt= 0.001s。 试验Δt= 0.001s和测试Δt= 0.002s和结果之间的差异是不明显的。 (注：在模拟中的系数值使用：$C_{D0} = 0.08，C_{Dα}= 2.72，C_{L0} = .15，C_{Lα}= 1.4)$

仿真结果

当进行模拟时，所有试验的初始高度为1m，初始x速度为14m/s，以及0m/s的初始y速度，这被认为是标准投掷飞盘的速度。试验使用从0°到45°的攻角。这是唯一的参数被改变，因为升力系数和阻力仅取决于攻角。从图2，图3可以看出和图4攻角对飞盘轨迹有很大的影响。具有低攻角（一般小于5度）升力非常小，飞盘快速下落到地面后短距离，通常小于20米。具有较大的攻角，更大的升力显然和飞盘更大高度和进一步行进，达40米。达到最大距离的攻角约为12°它行驶40米，最大高度为7.7米。在较大的攻角发射飞盘高度会更高，但由于阻力大，飞行距离较小。试验进行不同的初始速度跟随与具有初始速度的趋势相似的趋势速度为14m/s。在较低的速度下，提升力大大降低，飞盘会更快地掉到地上。在更高的速度提升力更大，轨迹越来越长。

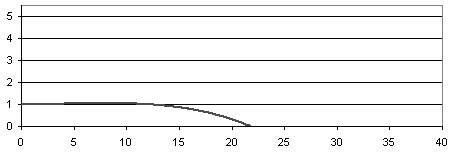
frisbee
Figure 3. Plot of height(m) versus distance(m) for a Frisbee with initial velocity 14
m/s and angle of attack 7.5◦
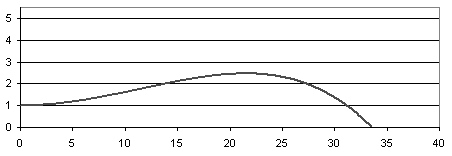
frisbee
Figure 2. Plot of height(m) versus distance(m) for a Frisbee with initial velocity 14
m/s and angle of attack 5◦
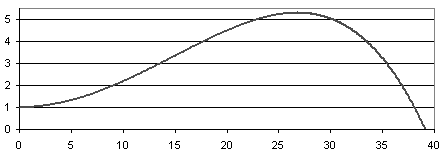
frisbee
Figure 4. Plot of height(m) versus distance(m) for a Frisbee with initial velocity 14
m/s and angle of attack 10◦

C++代码如下:
Frisbee.hpp文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#ifndef FRISBEE_H
#define FRISBEE_H

#define PI 3.1415926

class Frisbee
{
public:
    static void simulate(double y0, double vx0, double vy0, double alpha, double deltaT);
private:
    static double x;
    static double y;
    static double vx;
    static double vy;
    static const double g;      //
    static const double m;      //
    static const double RHO;    //
    static const double AREA;   //
    static const double CL0;    //
    static const double CLA;    //
    static const double CD0;    //
    static const double CDA;    //
    static const double ALPHA0; //
};

#endif

Frisbee.cpp文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include"Frisbee.h"
#include<math.h>
#include<iostream>
#include<fstream>
#include<string>
using namespace std;

const double Frisbee::g = -9.81;
const double Frisbee::m = 0.175;
const double Frisbee::RHO = 1.23;
const double Frisbee::AREA = 0.0568;
const double Frisbee::CL0 = 0.1;
const double Frisbee::CLA = 1.4;
const double Frisbee::CD0 = 0.08;
const double Frisbee::CDA = 2.72;
const double Frisbee::ALPHA0 = -4;
double Frisbee::vx = 0;
double Frisbee::vy = 0;
double Frisbee::x = 0;
double Frisbee::y = 0;

void Frisbee::simulate(double y0, double vx0, double vy0, double alpha, double deltaT)
{
    //通过S. A. Hummel给出的公式计算计算升力系数
    double cl = CL0 + CLA*alpha*PI / 180;
    //通过Prantl’s关系计算阻力
    double cd = CD0 + CDA*pow((alpha - ALPHA0)*PI / 180, 2);
    //初始化x位置
    x = 0;
    //初始化y位置
    y = y0;
    //初始化x方向速度 vx = vx0
    vx = vx0;
    //初始化x方向速度 vy = vy0
    vy = vy0;
    try{
        //将计算结果输出到一个word表格
        //PrintWriter pw = new PrintWriter(new BufferedWriter
        //  (new FileWriter("frisbee.csv")));

        ofstream fout;
        fout.open("frisbee.csv", ios_base::app);
        if (!fout.is_open())
        {
            throw "文件打开失败!";
        }

        //循环计数
        int k = 0;
        //一个while循环，执行迭代直到y位置达到零（即飞盘击中地面）
        while (y > 0){
            //在y方向上的速度变化获得将净力等于重力和提升力的总和并求解delta v
            double deltavy = (RHO*pow(vx, 2)*AREA*cl / 2 / m + g)*deltaT;
            //通过求解增量v的力方程（存在的唯一力是牵引力）获得x方向上的速度变化。
            double deltavx = -RHO*pow(vx, 2)*AREA*cd*deltaT;
            //新的位置和速度使用简单的力学计算。
            vx = vx + deltavx;
            vy = vy + deltavy;
            x = x + vx*deltaT;
            y = y + vy*deltaT;
            //只有每十次迭代的输出将被发送到电子表格，以便减少数据点的数量。
            if (k % 10 == 0){
                //pw.print(x + "," + y + "," + vx);
                fout << x << "," << y << "," << vx;
                //pw.println();
                //fout << "\r\n";
                fout << "\n";
                fout.flush();
            }
            k++;
        }
        fout.close();
    }
    catch (string s){
        cout << s + "Error, file frisbee.csv is in use.";
    }
}

int main()
{
    Frisbee::simulate(1, 16.5, 0, 6, 0.001);

    return 0;
}

因为实际需要进行翻译，如有不足，欢迎指正.

数学建模
飞盘 建模

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！