极线约束

三维空间中一点P，投影到两个不同的平面$I_{1}、I_{2}$，投影点分别为$P_{1}，P_{2}$。
$P、P_{1}、P_{2}$在三维空间内构成一个平面S。
S与面$I_{1}$的交线$L_{1}$过$P_{1}$点，称之为对应于$P_{2}$的极线。同理S与$I_{2}$的交线称之为对应于$P_{1}$的极线（对应于左边图像点的极线在右边图像上，右边与之相同）.

如图：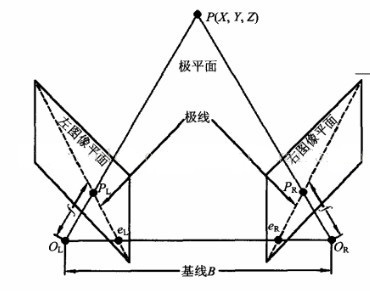

所谓极线约束就是说同一个点在两幅图像上的映射，已知左图映射点$P_{1}$，那么右图映射点$P_{2}$一定在相对于$P_1$的极线上，这样可以减少待匹配的点数量。

对于极线约束方程可以由以下来表示,三维向量x和x’存放相关点，F为一个3*3且秩为2的基础矩阵，那么：
$$ x’^T Fx = 0 ​$$
且左右两个平面的两条极线的方程为（注意 ’）：
$$ Ie = Fx ​$$
$$ Ie’ = F^T x’ ​$$
对于两条直线，以连续点的方式存储：I和I’分别在左右两幅图像上，若他们俩有对应关系，那么认为他们两条直线之间的点依次的存在对应关系。
对于左侧图像中直线I上的一点x，那么对应于右侧图像中直线I’中的点x’可以按照下面方式求得：
对应于x的极线为I’e，I’e与直线I’的交点为x对应的点x’因此：
$$ x’=I’\times Ie’=I’\times (Fx) ​$$