双线性插值

简介

双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。
假设源图像大小为$m\times n$，目标图像为$a \times b$。那么两幅图像的边长比分别为：$m/a$和$n/b$。注意，通常这个比例不是整数，编程存储的时候要用浮点型。目标图像的第（i,j）个像素点（i行j列）可以通过边长比对应回源图像。其对应坐标为`（i * m/a,j * n/b）。显然，这个对应坐标一般来说不是整数，而非整数的坐标是无法在图像这种离散数据上使用的。双线性插值通过寻找距离这个对应坐标最近的四个像素点，来计算该点的值（灰度值或者RGB值）。

原理

若图像为灰度图像，那么（i，j）点的灰度值的数学计算模型是：
$$ f(x,y)=b_{1}+b_{2}x+b_{3}y+b_{4}xy $$
其中$b_{1},b_{2},b_{3},b_{4}$是相关的系数。关于其的计算过程如下如下：
如图，已知$Q_{12}，Q_{22}，Q_{11}，Q_{21}$，但是要插值的点为P点，这就要用双线性插值了，首先在x轴方向上，对$R_1$和$R_2$两个点进行插值，这个很简单，然后根据$R_{1}$和$R_{2}$对$P$点进行插值，这就是所谓的双线性插值。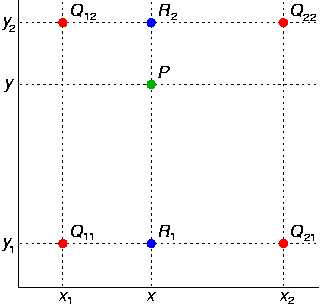

附：维基百科–双线性插值：
双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。
假如我们想得到未知函数f在点P=(x,y)的值，假设我们已知函数f在$Q_{11}=(x_{1},y_{1}),Q_{12}=(x_{1},y_{2}),Q_{21}=(x_{2},y_{1}),Q_{22}=(x_{2},y_{2})$四个点的值。
首先在 x 方向进行线性插值，得到
$$ f(R_{1})\approx \frac{x_{2}-x}{x_{2}-x_{1}} f(Q_{11}) + \frac{x-x_{1}}{x_{2}-x_{1}} f(Q_{21}) \leftarrow R_{1}=(x,y_{1}) $$
$$ f(R_{2})\approx \frac{x_{2}-x}{x_{2}-x_{1}} f(Q_{12}) + \frac{x-x_{1}}{x_{2}-x_{1}} f(Q_{22}) \leftarrow R_{1}=(x,y_{2}) $$
然后在 y 方向进行线性插值，得到
$$ f(P)\approx \frac{y_{2}-y}{y_{2}-y_{1}} f(R_{1}) + \frac{y-y_{1}}{y_{2}-y_{1}} f(R_{2}) $$
这样就得到所要的结果f(x,y),
$$ f(x,y) \approx \frac{Q_{11}}{(x_{2}-x_{1})(y_{2}-y_{1})} (x_{2}-x)(y_{2}-y) + \frac{Q_{21}}{(x_{2}-x_{1})(y_{2}-y_{1})} (x-x_{1})(y-y_{1}) $$
如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为:
$$ f(x,y) \approx f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy $$
或者用矩阵运算表示为:
$$
f(x,y) \approx [1-x \ x]
\begin{bmatrix}
f(0,0) & f(0,1) \
f(1,0) & f(1,1)
\end{bmatrix}
\begin{bmatrix}
1-y\
y
\end{bmatrix}
$$
这种插值方法的结果通常不是线性的，线性插值的结果与插值的顺序无关。首先进行 y 方向的插值，然后进行 x 方向的插值，所得到的结果是一样的。

源码实现

那么根据原理借助Opencv的Mat数据结构通过c++实现源码如下:

#include "opencv2/objdetect/objdetect.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/opencv.hpp"
#include <iostream>
#include <stdio.h>

using namespace std;
using namespace cv;

//srcX = dstX * (srcWidth /dstWidth)
//srcY = dstY * (srcHeight/dstHeight)
//f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1);
int main()
{
    double scale = 0.5;
    double srcX = 0;
    double srcY = 0;
    int Int_tmp_x = 0;
    double Dot_tmp_x = 0;
    int Int_tmp_y = 0;
    double Dot_tmp_y = 0;
    Mat src = imread("./res/lena.jpg", 0);
    Mat dst(scale * src.cols, scale * src.rows, src.type());
    for (double x = 0; x < src.cols * scale - (int)scale; x++)
    {
        for (double y = 0; y < src.rows * scale - (int)scale; y++)
        {
            if (x == 0 && y == 0)
                dst.at<char>(x, y) = src.at<char>(x, y);
            else
            {
                srcX = x / scale;
                Int_tmp_x = (int)srcX;
                Dot_tmp_x = srcX - Int_tmp_x;

                srcY = y / scale;
                Int_tmp_y = (int)srcY;
                Dot_tmp_y = srcY - Int_tmp_y;

                dst.at<uchar>(x, y) =
                    (1 - Dot_tmp_x)*(1 - Dot_tmp_y)*src.at<uchar>(Int_tmp_x, Int_tmp_y) +
                    (1 - Dot_tmp_x)*Dot_tmp_y*src.at<uchar>(Int_tmp_x, Int_tmp_y + 1) +
                    Dot_tmp_x*(1 - Dot_tmp_y)*src.at<uchar>(Int_tmp_x + 1, Int_tmp_y) +
                    Dot_tmp_x*Dot_tmp_y*src.at<uchar>(Int_tmp_x + 1, Int_tmp_y + 1);
            }
        }
    }
    cout << dst.size() << endl;
    //imwrite("./res/lena_large.jpg", dst);
    imshow("Dst",dst);
    waitKey();
    return 0;
}