一维信号的高斯滤波

正态分布

高斯滤波使用的是高斯函数，即我们熟悉的正态分布的概率密度函数：
$$ f(x)=\frac{1}{σ\sqrt{2π}} exp (\frac{(x-μ)^2}{2σ^2}) $$

我们生成的高斯模板就是从这个公式来的。例如要生成一个大小为3，标准差为1的模板，则只需要代公式计算（此处均值μ为0，不为0将其平移即可）：$f(−1) 、f(0)、f(1)$就可以得到模板的值了。

高斯滤波是如何实现的？

其实思想很简单，高斯分布的特点是在均值μ两边的概率都很大，离之越远的概率越小，所以高斯函数用在滤波上体现的思想就是：离某个点越近的点对其产生的影响越大，所以让其权重大，越远的产生的影响越小，让其权重越小。

举个例子，有如下一个序列，对其中的6进行操作，模板为[1,2,1]：

1 2 3 5 6 3 1 7 5 3 8 
        |
      1 2 1

那么结果为：(5x1+6x2+3x1)/(1+2+1)=5 ，对每个数据都进行这样的操作，就是所谓的高斯滤波了。
有一个问题，如果是开头和结尾怎么办？
一种做法是补0：

0 1 2 3 5 6 3 1 7 5 3 8 
  |
1 2 1

另一种做法就是不让模板超出信号的范围，此处采用后一种做法。

matlab代码

高斯滤波函数Gaussianfilter：

% 功能：对一维信号的高斯滤波，头尾r/2的信号不进行滤波
% r     :高斯模板的大小推荐奇数
% sigma :标准差
% y     :需要进行高斯滤波的序列
function y_filted = Gaussianfilter(r, sigma, y)

% 生成一维高斯滤波模板
GaussTemp = ones(1,r*2-1);
for i=1 : r*2-1
    GaussTemp(i) = exp(-(i-r)^2/(2*sigma^2))/(sigma*sqrt(2*pi));
end

% 高斯滤波
y_filted = y;
for i = r : length(y)-r
    y_filted(i) = y(i-r+1 : i+r-1)*GaussTemp';
end

测试代码：

% 测试数据
x = 1:50;
y = x + rand(1,50)*10;

% 设置高斯模板大小和标准差
r        = 3;
sigma    = 1;
y_filted = Gaussianfilter(r, sigma, y);

% 作图对比
plot(x, y, x, y_filted);
title('高斯滤波');
legend('滤波前','滤波后','Location','northwest')

如何使用？
新建2个m文件，一个命名为Gaussianfilter，把第一段代码复制进去；另一个命名为testgauss，把第二段代码复制进去，保存。在testgauss中点击运行按钮，即可看到结果。
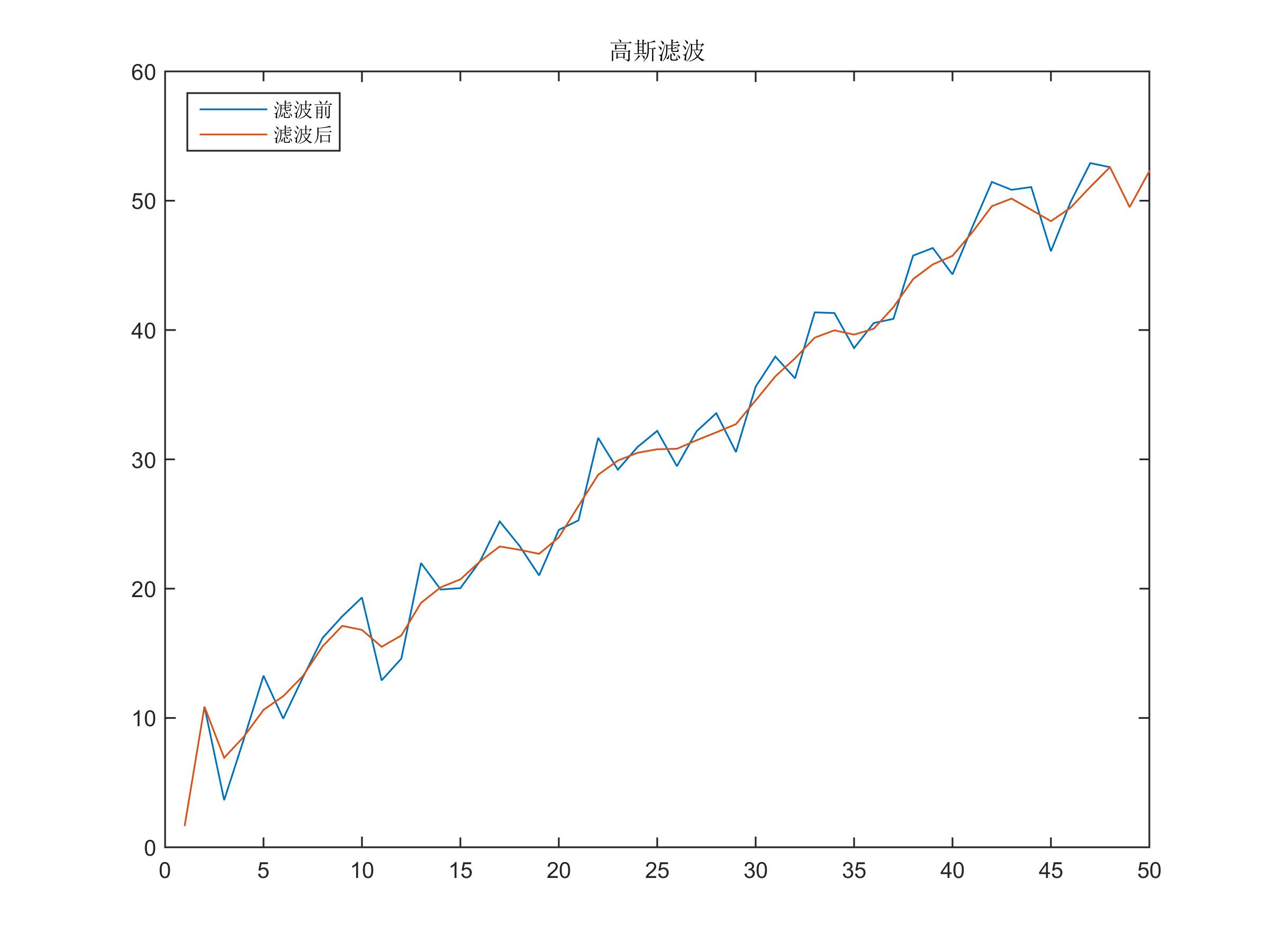
结果：