逻辑回归模型和ML入门

简介(Introduction)

问题：肿瘤医院提供了数据，并希望我们确定患者是否有致命的恶性肿瘤或良性肿瘤。 这被称为分类问题。 为了帮助分类每个患者，我们给出他们的年龄和肿瘤的大小。 直观地，可以想象年轻的患者和患有小的良性肿瘤的患者不太可能患有恶性癌症。 数据集模拟此应用程序，其中每个观察结果是表示为点（在下面的图中）的患者，其中红色表示恶性，蓝色表示良性。 注意：这是一个学习的玩具示例，在现实生活中有大量来自不同测试(检查)源的特征和医生的经验，这些特征对患者的诊断(治疗)决定起作用。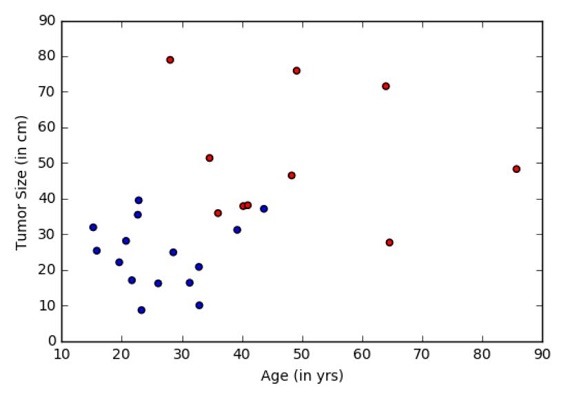
image1
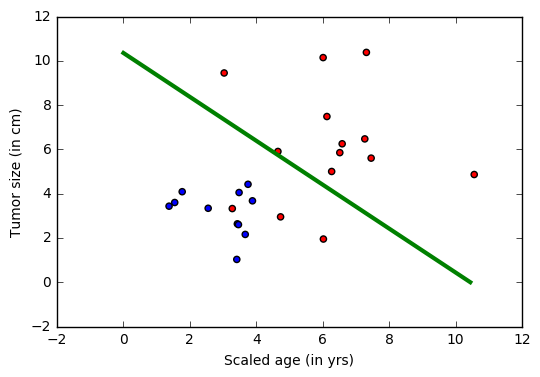
目标：我们的目标是训练一个分类器，可以根据两个特征（年龄和肿瘤大小）自动将任何患者标记为良性或恶性类别。 本次，我们将创建一个线性分类器，它是深度网络中的一块基石。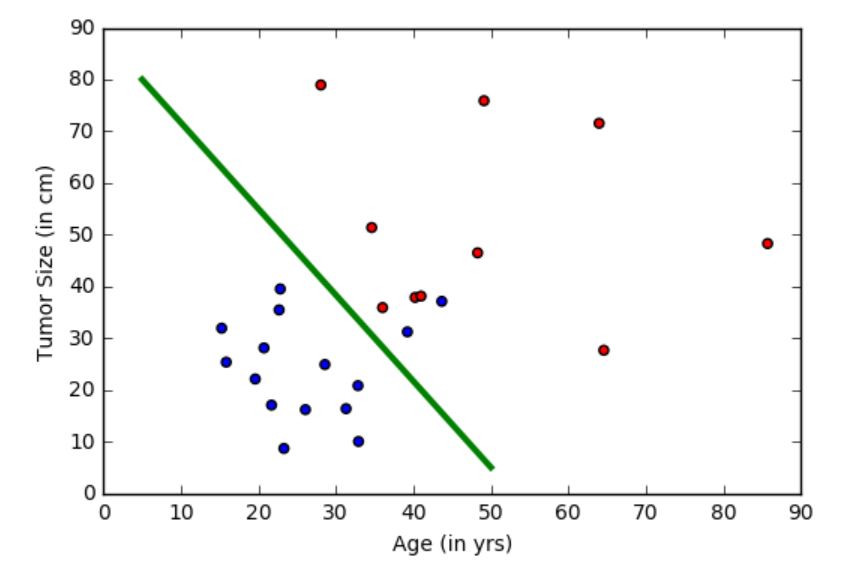
image2
在上图中，绿线表示从数据中学习的模型，并将蓝点与红点分离。注意：这个分类器确实犯错误，其中蓝色点在绿色线的错误一侧。 但是，有办法解决这个问题，既是用非线性分类来解决。
方法：任何学习算法通常具有五个阶段。数据读取，数据预处理，模型创建，模型参数学习和模型评估(模型测试或模型预测)。

  • 1.**数据读取(Data reading)**：我们生成的模拟数据集，每个样品具有指示年龄和肿瘤大小的两个特征（绘制如下）。
  • 2.**数据预处理(Data Preprocessing)**：通常需要对尺寸或年龄等个别特征进行缩放。 通常，可以在0和1之间缩放数据。为了简单起见，本次不进行任何缩放（有关详细信息，请参阅：特征缩放）。
  • 3.**模型创建(Model creation)**：本次我们创建一个基本的线性模型。
  • 4.模型学习(Learing the model)：这也被称为训练。虽然拟合线性模型可以以各种方式（线性回归），在CNTK中，我们使用随机梯度下降SGD。
  • 5.**评估(Evaluation)**：这也被称为测试，其中采用具有未曾用于训练的已知标签（也称ground-truth）的数据集。 这使我们能够评估模型在现实世界（以前看不到的）观察中的表现。

逻辑回归(Logistic Regression)

逻辑回归(Logistic Regression)是使用特征的线性加权组合并且预测不同类的概率的基本机器学习技术。 在我们的情况下，分类器将在[0,1]中生成概率，然后与阈值（例如0.5）进行比较以产生二进制标签（0或1）。显然，所示的方法可以容易地扩展到多个类。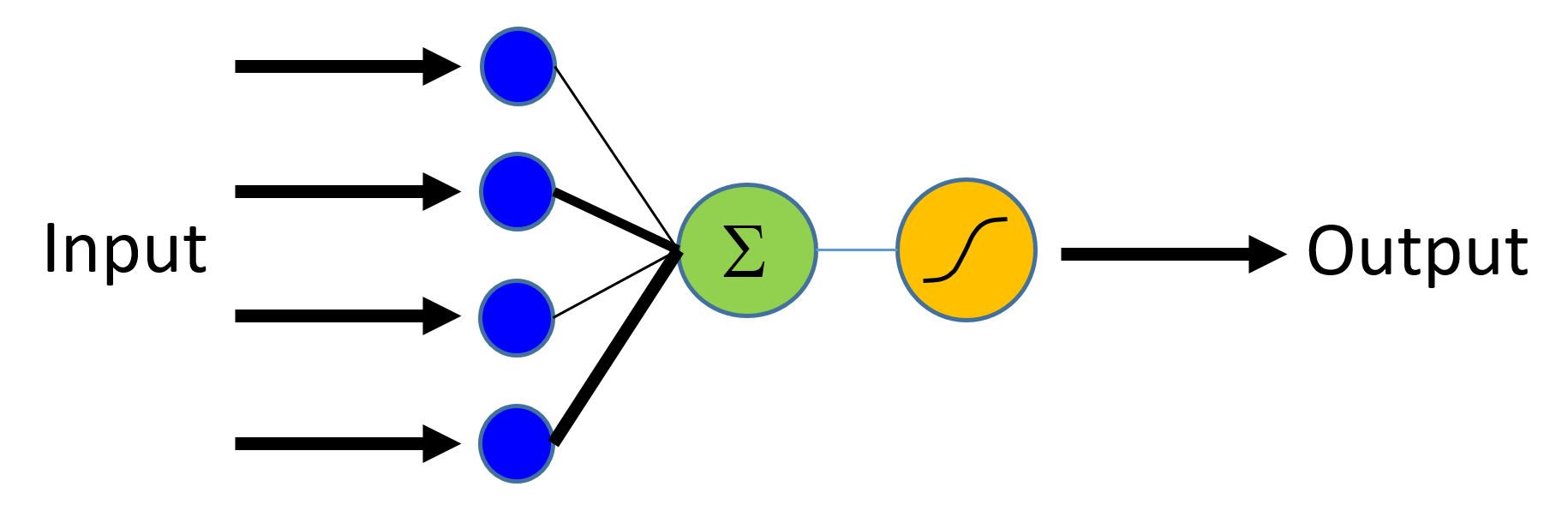
image3
在上图中，来自不同输入特征的贡献被线性加权并且聚合。 所得的总和通过sigmoid函数映射到0-1范围。 对于具有多于两个输出标签的分类器，可以使用[softmax][]函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Import 相关组件
from __future__ import print_function
import numpy as np
import sys
import os
from cntk import Trainer, learning_rate_schedule, UnitType
from cntk.learner import sgd
from cntk.ops import *
# 在测计算机时选择正确的目标设备：
if 'TEST_DEVICE' in os.environ:
    import cntk
    if os.environ['TEST_DEVICE'] == 'cpu':
        cntk.device.set_default_device(cntk.device.cpu())
    else:
        cntk.device.set_default_device(cntk.device.gpu(0))

数据生成(Data Generation)

将使用numpy库生成一些模拟肿瘤示例的合成数据。我们有两个特征（以二维表示），每个特征都是两个类别中的一个（蓝色点:良性、红色点:恶性）。
训练数据中的每个表观(observation)具有对应于每个表观(observation)（特征 - 年龄和大小的集合）的标签（蓝色或红色）。 在这个例子中，我们有两个类由标签0或1表示，因此这是个二进制分类任务。

1
2
3
# 定义该网络
input_dim = 2
num_output_classes = 2

输入(Input)和标签(Labels)

在本示例中，我们使用numpy库来生成合成数据。在现实世界的问题中，将使用读取器，其将读取对应于每个观察（患者）的特征值（特征：年龄和肿瘤大小）。模拟的年龄变量按比例缩小使其具有与其他变量类似的范围。这是数据预处理的一个关键方面。**注意:**每个表观(observation)可以处在更高维度的空间中（当更多特征可用时），并且将在CNTK中表示为张量(tensor)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 确保我们总是获得相同的随机性
np.random.seed(0)

# 辅助函数生成随机数据样本
def generate_random_data_sample(sample_size, feature_dim, num_classes):
    # 使用NumPy创建合成数据
    Y = np.random.randint(size=(sample_size, 1), low=0, high=num_classes)

    # 确保数据是可分离的 
    X = (np.random.randn(sample_size, feature_dim)+3) * (Y+1)
    
    # 指定数据类型以匹配后面使用的输入变量 
    # (默认double类型)
    X = X.astype(np.float32)    
    
    # 将类 0 转换为向量 '1 0 0'
    # 类 1 转换为向量 '0 1 0', ...
    class_ind = [Y==class_number for class_number in range(num_classes)]
    Y = np.asarray(np.hstack(class_ind), dtype=np.float32)
    return X, Y   
1
2
3
4
# 创建表征要素和标签数据的输入变量。 
#注意：input_variable不需要关于观察值（样本）的附加信息，因为CNTK首先仅创建网络拓扑
mysamplesize = 32
features, labels = generate_random_data_sample(mysamplesize, input_dim, num_output_classes)

接下来可视化数据处理。
注意：如果matplotlib.pyplot的导入失败，请运行conda install matplotlib，这将修复pyplot版本依赖性。 如果你在一个不同于Anaconda的python环境中，那么使用pip install。

1
2
3
4
5
6
7
8
9
# 绘制数据
import matplotlib.pyplot as plt
# 给定一个2分类
colors = ['r' if l == 0 else 'b' for l in labels[:,0]]

plt.scatter(features[:,0], features[:,1], c=colors)
plt.xlabel("Scaled age (in yrs)")
plt.ylabel("Tumor size (in cm)")
plt.show()

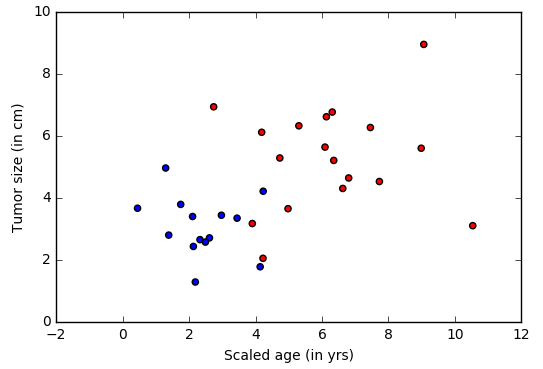
image4

模型创建(Model Creation)

逻辑回归网络（又名LR）是最简单的构建块，但x在过去十年中已经为许多ML应用程序提供了动力。 LR是一个简单的线性模型，它以一个数字向量作为输入，描述我们所分类的属性（也称为特征向量X，下图中的蓝色节点），并发出Evidence(Z)(从绿色节点发出，也称为激活）。输入层中的每个特征通过相应的权重w（由不同厚度的黑线表示）与输出节点连接。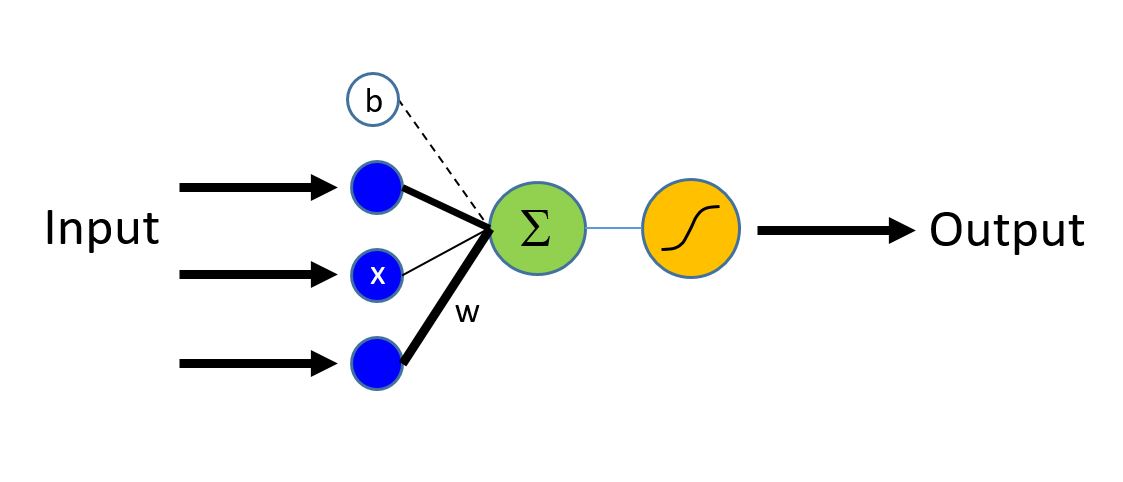
image5

第一步是计算观察的证据(evidence)。
$$z = \sum_{i=1}^n w_i \times x_i + b = \textbf{w} \cdot \textbf{x} + b$$
$\bf{w}$ 是长度的权重向量. $b$ 是偏差项.
Note: 使用粗体表示法来表示向量。
使用sigmoid(当结果可以取两个值之一时)或softmax函数(当结果可以采用多于2个类别值中的一个时)，将所计算的证据映射到0-1标度。
**输入变量(a key CNTK概念)**：输入变量是面向用户代码的容器，其中用户提供的代码在模型学习(aka training)期间填充不同的观察(数据点或样本，在本示例中等同于蓝色/红色点)作为模型函数的输入， 模型评价(测试)。 因此，input_variable的形状必须匹配将提供的数据的形状。 例如，当数据是高度10像素和宽度5像素的图像时，输入特征尺寸将是2(表示图像高度和宽度)。类似地，在我们的示例中，维度是年龄和肿瘤大小，因此input_dim=2.更多关于数据及其维度，以显示在单独的教程中。

input = input_variable(input_dim, np.float32)

网络设置(Network Setup)

linear_layer函数是上述方程的直接实现。 我们执行两个操作：

  • 1.使用CNTK乘法运算符将权重($\bf{w}$)与特征($\bf{x}$)相乘，并且添加个体特征的贡献(contribution)
  • 2.添加偏差项b

这些CNTK操作被优化并在可用硬件上执行，并且隐藏了，实现减少用户使用的复杂性。

1
2
3
4
5
6
7
8
9
10
11
12
13
# 定义字典以存储模型参数
mydict = {"w":None,"b":None} 
def linear_layer(input_var, output_dim):
    input_dim = input_var.shape[0]
    weight_param = parameter(shape=(input_dim, output_dim))
    bias_param = parameter(shape=(output_dim))
    mydict['w'], mydict['b'] = weight_param, bias_param
    return times(input_var, weight_param) + bias_param   

# z代表网络的输出

output_dim = num_output_classes
z = linear_layer(input, output_dim)

训练模型参数(Learning model parameters)

现在网络已经建立，我们想学习我们的简单线性层的参数$\bf{w}$和b。 为此，我们使用softmax函数将计算的证据(evidence)z转换为一组预测概率($\bf{P}$)。

$$ \textbf{p} = \mathrm{softmax}(z)$$

softmax是将累积的证据(evidence)映射到类别上的概率分布(softmax)的激活函数。 激活功能的其他选择可以在这里找到。

训练(Training)

softmax的输出是属于各个类别的观察(observation)的概率。 为了训练分类器，我们需要确定模型需要模拟的行为。 换句话说，我们希望生成的概率尽可能接近观察到的标签。 此函数称为成本或损失函数，并显示学习模型与由训练集生成的模型之间的差异。
交叉熵(Cross-entropy)是衡量损失的常用函数。 它定义为：
$$ H(p) = - \sum_{j=1}^C y_j \log (p_j) $$
其中$p$是我们从softmax函数的预测概率，$y$表示标签。 提供用于训练的数据的该标签也称为**地面真值(ground-truth)**标签。 在两类示例中，标签变量具有两个维度（等于num_output_classes或$C$）。 一般来说，如果手中的任务需要分类到$C$不同的类，则标签变量将具有除了由数据点表示的类别1之外的所有地方的$C$元素。强烈推荐到Blog理解这个交叉熵函数的细节。

1
2
label = input_variable((num_output_classes), np.float32)
loss = cross_entropy_with_softmax(z, label)

测试(Evaluation)

为了评估分类，可以比较网络的输出，其对于每个观察发射(emits)具有等于类的数量的维度的证据的向量（可以使用softmax函数转换成概率）。

1
eval_error = classification_error(z, label)

配置训练(Configer Training)

训练者努力通过不同的优化方法减少损失函数，随机梯度下降（sgd）是最流行的一种。通常，可以从模型参数的随机初始化开始。sgd优化器将计算预测标签与相应的地面真值标签之间的损失或误差，并使用gradient-decent在单次迭代中生成新的集合模型参数。一次使用单个观察的上述模型参数更新是有吸引力的，因为其不需要将整个数据集（所有观察）加载到存储器中，并且还需要在较少数据点上的梯度计算，从而允许对大数据集进行训练。然而，使用单个观察样本一次产生的更新在迭代之间可以非常不同。中间点是加载一小组观测值，并使用来自该组的损失或误差的平均值来更新模型参数。这个子集称为minibatch。使用minibatches我们经常从较大的训练数据集采样观察。我们重复模型参数更新的过程，使用不同的训练样本组合，并在一段时间内使损失（和误差）最小化。当增量误差率不再显着变化或在预设数量的最大微型间隔训练之后，我们声称我们的模型是训练的。优化的关键参数之一称为learning_rate。现在，我们可以把它看作是一个缩放因子，它可以调节我们在任何迭代中改变参数的程度。我们将在后面的教程中介绍更多的细节。有了这些信息，我们随时准备创建我们的训练器。

1
2
3
4
5
# 实例化训练器对象以驱动模型训练
learning_rate = 0.5
lr_schedule = learning_rate_schedule(learning_rate, UnitType.minibatch) 
learner = sgd(z.parameters, lr_schedule)
trainer = Trainer(z, (loss, eval_error), [learner])

首先让我们创建一些帮助函数，可视化与训练相关的不同功能。 注意这些令人信服的功能是为了理解其内部机理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from cntk.utils import get_train_eval_criterion, get_train_loss

# 定义一个效用函数来计算移动平均和。
# 使用np.cumsum（）函数可以实现更高效的实现
def moving_average(a, w=10):
    if len(a) < w: 
        return a[:]    
    return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)]
# 定义打印训练进度的函数
def print_training_progress(trainer, mb, frequency, verbose=1):
    training_loss, eval_error = "NA", "NA"

    if mb % frequency == 0:
        training_loss = get_train_loss(trainer)
        eval_error = get_train_eval_criterion(trainer)
        if verbose: 
            print ("Minibatch: {0}, Loss: {1:.4f}, Error: {2:.2f}".format(mb, training_loss, eval_error))
        
    return mb, training_loss, eval_error

运行训练器(Run the trainer)

我们现在准备训练我们的逻辑回归模型。 我们想决定我们需要将什么数据输入到训练引擎中。
在此示例中，优化程序的每次迭代将工作在25个样本（25点w.r.t.上面的图）a.k.a. minibatch_size。 我们想训练说20000个观察。 如果数据中的样本数量只有10000，训练器将使2次通过数据。 这由num_minibatches_to_train表示。注意：在现实世界的情况下，我们将被给予一定量的标记数据（在本示例的上下文中，观察（年龄，大小）及其意义（良性/恶性）。 我们将使用大量的训练观察值表示70％，并留出余下的值用于评估训练模型。
利用这些参数，我们可以继续训练我们的简单前馈网络。

1
2
3
4
# Initialize the parameters for the trainer
minibatch_size = 25
num_samples_to_train = 20000
num_minibatches_to_train = int(num_samples_to_train  / minibatch_size)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Run the trainer and perform model training
training_progress_output_freq = 50

plotdata = {"batchsize":[], "loss":[], "error":[]}

for i in range(0, num_minibatches_to_train):
    features, labels = generate_random_data_sample(minibatch_size, input_dim, num_output_classes)
    
    # Specify input variables mapping in the model to actual minibatch data to be trained with
    trainer.train_minibatch({input : features, label : labels})
    batchsize, loss, error = print_training_progress(trainer, i, 
                                                     training_progress_output_freq, verbose=1)
    
    if not (loss == "NA" or error =="NA"):
        plotdata["batchsize"].append(batchsize)
        plotdata["loss"].append(loss)
        plotdata["error"].append(error)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Minibatch: 0, Loss: 0.6931, Error: 0.32
Minibatch: 50, Loss: 2.4317, Error: 0.36
Minibatch: 100, Loss: 0.4701, Error: 0.20
Minibatch: 150, Loss: 0.7732, Error: 0.40
Minibatch: 200, Loss: 0.1273, Error: 0.04
Minibatch: 250, Loss: 0.1316, Error: 0.08
Minibatch: 300, Loss: 0.1012, Error: 0.04
Minibatch: 350, Loss: 0.1071, Error: 0.04
Minibatch: 400, Loss: 0.3085, Error: 0.08
Minibatch: 450, Loss: 0.3214, Error: 0.12
Minibatch: 500, Loss: 0.4114, Error: 0.20
Minibatch: 550, Loss: 0.6799, Error: 0.20
Minibatch: 600, Loss: 0.2982, Error: 0.12
Minibatch: 650, Loss: 0.1675, Error: 0.12
Minibatch: 700, Loss: 0.2770, Error: 0.12
Minibatch: 750, Loss: 0.2308, Error: 0.04
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Compute the moving average loss to smooth out the noise in SGD
plotdata["avgloss"] = moving_average(plotdata["loss"])
plotdata["avgerror"] = moving_average(plotdata["error"])

# Plot the training loss and the training error
import matplotlib.pyplot as plt

plt.figure(1)
plt.subplot(211)
plt.plot(plotdata["batchsize"], plotdata["avgloss"], 'b--')
plt.xlabel('Minibatch number')
plt.ylabel('Loss')
plt.title('Minibatch run vs. Training loss')

plt.show()

plt.subplot(212)
plt.plot(plotdata["batchsize"], plotdata["avgerror"], 'r--')
plt.xlabel('Minibatch number')
plt.ylabel('Label Prediction Error')
plt.title('Minibatch run vs. Label Prediction Error')
plt.show()

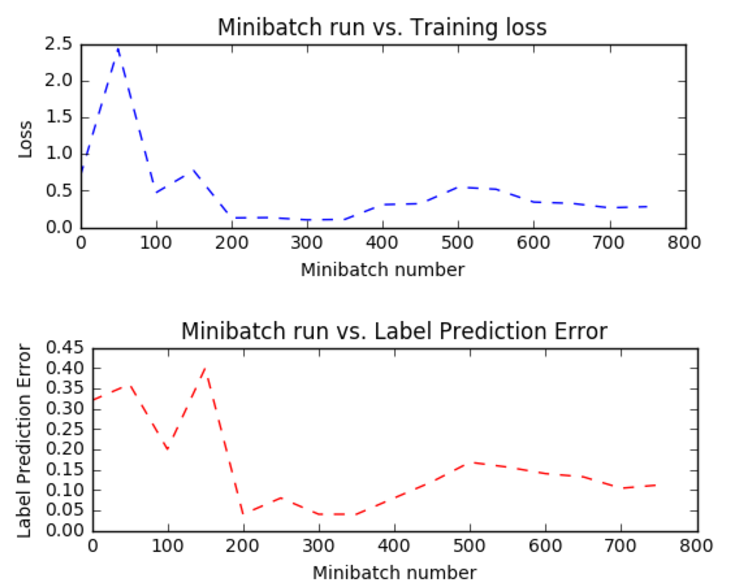
image6

评估测试(Evaluation/Testing)

现在我们已经训练了网络。 让我们评估训练网络对未用于训练的数据。 这称为测试。 让我们创建一些新的数据，并评估这个集合的平均错误和损失。 这是使用trainer.test_minibatch完成的。 注意，这个以前看不见的数据的错误与训练错误相当。 这是一个关键的检查。 如果误差大于训练误差大的幅度，则表明训练的模型在训练期间没有见到的数据上不能很好地执行。 这被称为过度拟合。 有几种方法来解决超额配合，这超出了本教程的范围，但认知工具包提供了必要的组件来解决过度拟合。
注意：为了说明的目的，我们正在测试一个小型批次。 在实践中，运行几个测试数据的小型批次并报告平均值。
问题:为什么这是建议？ 尝试使用用于训练的绘图函数在多组生成的数据样本和绘图上绘制测试错误。 你看到一个模式吗？

1
2
3
4
5
# Run the trained model on newly generated dataset
test_minibatch_size = 25
features, labels = generate_random_data_sample(test_minibatch_size, input_dim, num_output_classes)

trainer.test_minibatch({input : features, label : labels})

输出:0.12

检查预测/评估(Checking prediction/evaluation)

为了评估，我们将网络的输出在0-1之间映射，并将它们转换为两个类的概率。 这表明每次观察的机会是恶性和良性的。 我们使用softmax函数来获得每个类的概率。

1
2
out = softmax(z)
result = out.eval({input : features})

让我们将地面真实标签与预测进行比较。 他们应该符合。

Question:

  • 有多少预测被错误标记？ 您可以更改下面的代码，以确定哪些观察被错误分类？
    1
    2
    print("Label    :", [np.argmax(label) for label in labels])
    print("Predicted:", [np.argmax(result[i,:,:]) for i in range(result.shape[0])])
    Label : [1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1]
    Predicted: [1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1]

可视化(Visualization)

期望可视化结果。 在该示例中，数据方便地在二维中并且可以被绘制。 对于具有较高尺寸的数据，可视化可能具有挑战性。 存在允许这种可视化的先进的降维技术。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Model parameters
print(mydict['b'].value)

bias_vector   = mydict['b'].value
weight_matrix = mydict['w'].value

# Plot the data 
import matplotlib.pyplot as plt

# given this is a 2 class 
colors = ['r' if l == 0 else 'b' for l in labels[:,0]]
plt.scatter(features[:,0], features[:,1], c=colors)
plt.plot([0, bias_vector[0]/weight_matrix[0][1]], 
         [ bias_vector[1]/weight_matrix[0][0], 0], c = 'g', lw = 3)
plt.xlabel("Scaled age (in yrs)")
plt.ylabel("Tumor size (in cm)")
plt.show()

输出结果:[ 7.98766518 -7.988904 ]

image7

探索建议(Exploration Suggestions)

  • 尝试探索分类器如何与不同的数据分布行为，建议更改minibatch_size参数从25到说64.为什么错误增加？
  • 尝试探索不同的激活功能
  • 尝试探索不同的学习模型
  • 可以探索训练多类逻辑回归分类器。
Machine Learning
ML 逻辑回归模型

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！