Delaunay Triangle

Delaunay三角剖分特点：

最小角最大：在不出现奇异性的情况下,Delaunay三角剖分最小角之和均大于任何非 Delaunay剖分所形成三角形最小角之和 ,三角形的最小内角之和最大 ,从而使得划分的三角形不会出现某个内角过小的情况 ,比较有利于有限元的后续计算。
空外接圆：Delaunay三角剖分中任意三角形的外接圆内不包括其他结点。因此 ,在各种二维三角剖分中 ,只有 Delaunay三角剖分才同时满足全局和局部最优。

Delaunay三角剖分优点：

1.最接近：以最近的三点组成三角形，且三角形各边皆不相交。
2.唯一性：不论从何处区域开始构建，最终结果唯一。
3.最优解：任意两个相邻三角形形成的凸四边形的对角线若可以互换,那么两个三角形六个内角中最小的角度不会变大。
4.最规则：若将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大。
5.区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。
6.具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

Voronoi图

离散点集P的Delaunay三角剖分和离散点集P的Voronoi图为对偶图的关系。

Delaunay三角形的外心是Voronoi图的顶点。

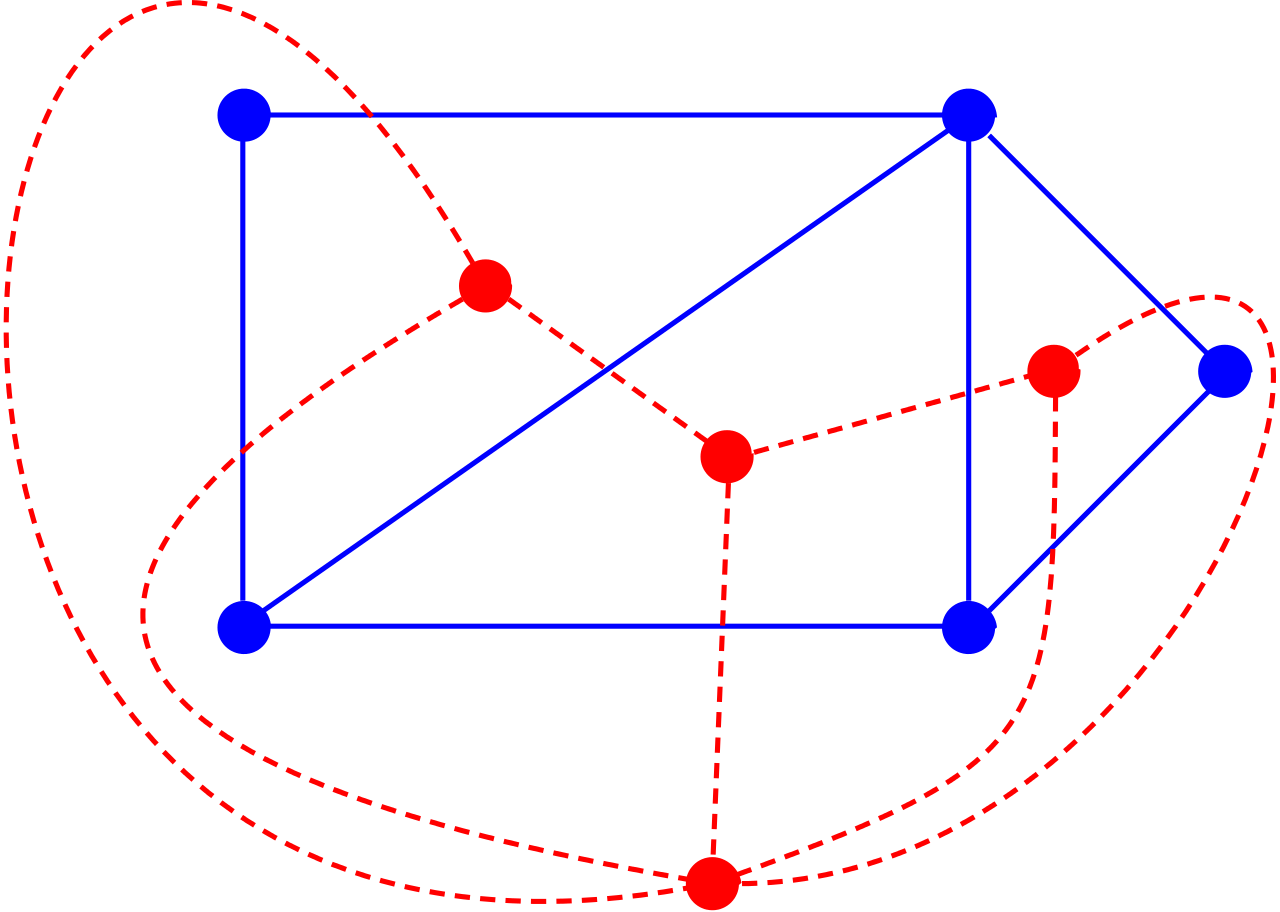
对偶图：设G是平面图，在图G的每个面中指定一个新节点，对两个面公共的边，指定一条新边与其相交。由这些新结点和新边组成的图为G的对偶图。

图中的蓝色虚线的图是红色实线的对偶图：

Duals_graphs

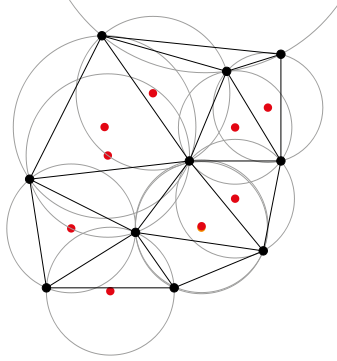
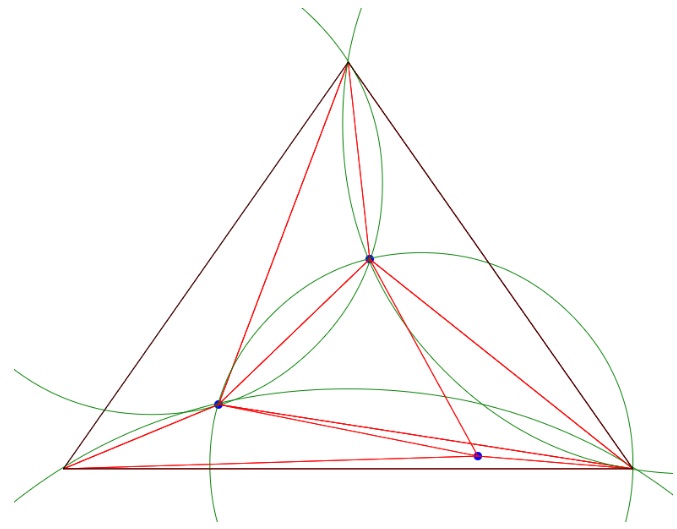
Delaunay三角形和其外接圆与圆心：

Delaunay_circumcircles_centers

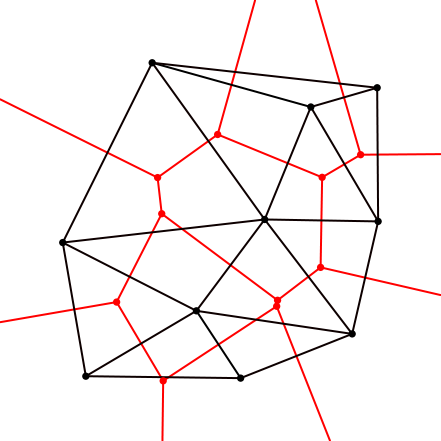
连接外接圆圆心生成Voronoi图：

Delaunay_Voronoi

Delaunay三角剖分算法

Delaunay三角剖分常见算法：翻边算法、分割归并法、逐点插入算法、三角网增长法。本文从常见的逐点插入的Bowyer-Watson算法来理解。

在《Triangulate》里对该方法进行了分析，给出了伪代码：

subroutine triangulate
input : vertex list
output : triangle list
   initialize the triangle list
   determine the supertriangle
   add supertriangle vertices to the end of the vertex list
   add the supertriangle to the triangle list
   for each sample point in the vertex list
      initialize the edge buffer
      for each triangle currently in the triangle list
         calculate the triangle circumcircle center and radius
         if the point lies in the triangle circumcircle then
            add the three triangle edges to the edge buffer
            remove the triangle from the triangle list
         endif
      endfor
      delete all doubly specified edges from the edge buffer
         this leaves the edges of the enclosing polygon only
      add to the triangle list all triangles formed between the point 
         and the edges of the enclosing polygon
   endfor
   remove any triangles from the triangle list that use the supertriangle vertices
   remove the supertriangle vertices from the vertex list
end

因该算法效率不高，因此有网上给的优化后的伪代码：

input: 顶点列表(vertices)　　　　　　　　　　　　　　　　　　　　  　//vertices为外部生成的随机或乱序顶点列表
output:已确定的三角形列表(triangles)
　　　　初始化顶点列表
　　　　创建索引列表(indices = new Array(vertices.length))　　　　//indices数组中的值为0,1,2,3,......,vertices.length-1
　　　　基于vertices中的顶点x坐标对indices进行sort　　  　　　　　  //sort后的indices值顺序为顶点坐标x从小到大排序（也可对y坐标，本例中针对x坐标）
　　　　确定超级三角形
　　　　将超级三角形保存至未确定三角形列表（temp triangles）
　　　　将超级三角形push到triangles列表
　　　　遍历基于indices顺序的vertices中每一个点　　　　　　　　　  　//基于indices后，则顶点则是由x从小到大出现
　　　　　　初始化边缓存数组（edge buffer）
　　　　　　遍历temp triangles中的每一个三角形
　　　　　　　　计算该三角形的圆心和半径
　　　　　　　　如果该点在外接圆的右侧
　　　　　　　　　　则该三角形为Delaunay三角形，保存到triangles
　　　　　　　　　　并在temp里去除掉
　　　　　　　　　　跳过
　　　　　　　　如果该点在外接圆外（即也不是外接圆右侧）
　　　　　　　　　　则该三角形为不确定        　　　　　　　　　     //后面会在问题中讨论
　　　　　　　　　　跳过
　　　　　　　　如果该点在外接圆内
　　　　　　　　　　则该三角形不为Delaunay三角形
　　　　　　　　　　将三边保存至edge buffer
　　　　　　　　　　在temp中去除掉该三角形
　　　　　　对edge buffer进行去重
　　　　　　将edge buffer中的边与当前的点进行组合成若干三角形并保存至temp triangles中
　　　　将triangles与temp triangles进行合并
　　　　除去与超级三角形有关的三角形
end

Bowyer-Watson算法

基本思想:

1.构造一个超级三角形，包含所有的散点，存入三角形链表
2.将点集中的离散点依次插入，在三角形链表中找出外接圆包含插入点的三角形（称为该点的影响三角形），删除影响三角形的公共边，将插入点同影响三角形的全部顶点连接起来，完成一个点在Delaunay三角形链表中的插入。
3.根据优化准则对局部新形成的三角形优化。将形成的三角形放入Delaunay三角形链表。
4.循环执行步骤2，直到所有离散点插入完毕。

图示:(来自百度百科)

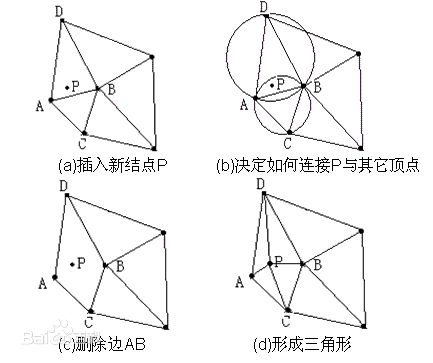
借助三个点理解一遍。

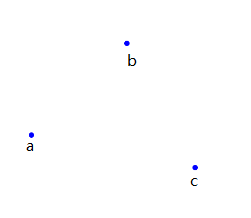
根据离散点的最大分布得到一个随机超级三角形(即该三角形包含了整个离散点集P)，并将超级三角形放入temp triangles中

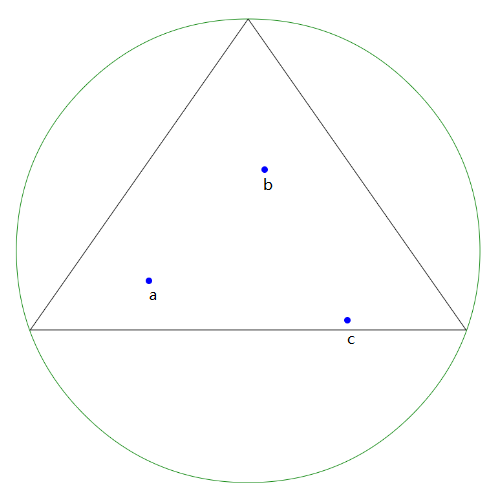
接下来对temp triangle中的三角形遍历画外接圆，这时先对左边第一个点a进行判断，其在圆内所以该三角形不为Delaunay三角形，将其三边保存至edge buffer中，temp triangles中删除该三角形

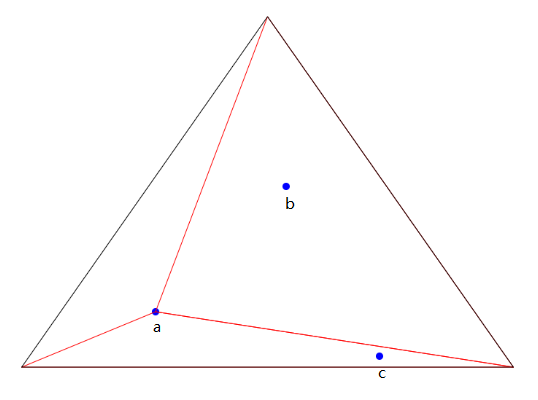
将a点与edge buffer中的每一个边相连，组成三个三角形，存入temp triangles中

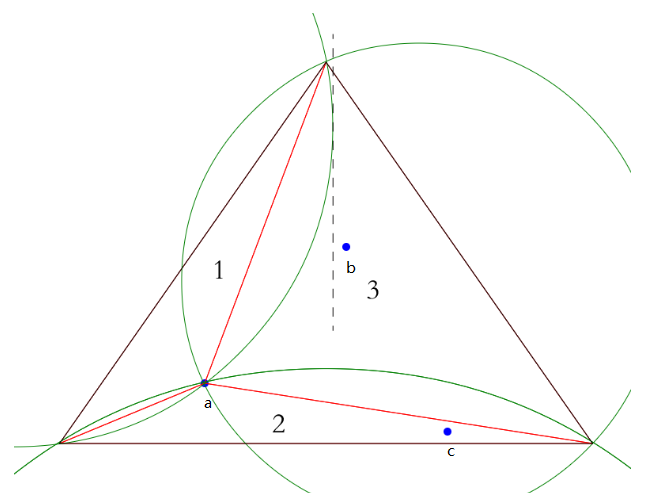
Delaunay三角剖分/Snipaste_2019-11-28_10-05-40.png

再将重复对temp triangles的遍历并画外接圆，这时使用的是b点来进行判断

b点在三角形1外接圆右侧，则表示左侧三角形为Delaunay三角形，将该三角形保存至triangles中
b点在三角形2外接圆外侧，为不确定三角形，跳过（后面处理），但并不在temp triangles中删除
b点在三角形3外接圆内侧，则这时向清空后的edge buffer加入该三角形的三条边，并用b点与edge buffer中的三角边进行组合，组合成了三个三角形并加入到temp triangles中

这时，temp buffer 中有六条边，triangles中有两个三角形，temp triangles中有1个三角形

对temp buffer中的六条边进行去重，得到五条边，将该点与这五条边组合成五个三角形并加入到temp triangles 中，这时temp triangles中有6个三角形

Delaunay三角剖分/Snipaste_2019-11-28_10-13-35.png