Jacobian矩阵与Hessian矩阵与最小二乘

雅可比矩阵 (Jacobian matrix)

在向量分析中, 雅可比矩阵是一阶偏导数以一定方式排列成的矩阵, 其行列式称为雅可比行列式. 还有, 在代数几何中, 代数曲线的雅可比量表示雅可比簇：伴随该曲线的一个代数群, 曲线可以嵌入其中. 它们全部都以数学家卡尔·雅可比(Carl Jacob, 1804年10月4日－1851年2月18日)命名；英文雅可比量”Jacobian”可以发音为[ja ˈko bi ən]或者[ʤə ˈko bi ən].

雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近. 因此, 雅可比矩阵类似于多元函数的导数.

假设$F:R_n→R_m$是一个从欧式n维空间转换到欧式m维空间的函数。这个函数由m个实函数组成:$ y_1(x_1,…,x_n), …, y_m(x_1,…,x_n)$. 这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵，这就是所谓的雅可比矩阵：
$$\begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n}\ \vdots & \ddots & \vdots \ \frac{\partial y_n}{\partial x_1} & \cdots & \frac{\partial y_n}{\partial x_n} \end{bmatrix}$$

此矩阵表示为：$J_F(x_1,\cdots ,x_2)$，或者:$\frac{\partial (y_1,\cdots,y_n)}{\partial (x_1, \cdots ,x_n)}$

这个矩阵的第$i$行是由梯度函数的转置$y_i(i=1,…,m)$表示的。

如果$p$是$R_n$中的一点, $F$在$p$点可微分, 那么在$p$这一点的导数由$J_{F(p)}$给出(这是求该点导数最简便的方法). 在此情况下, 由$F_(p)$描述的线性算子即接近点$p$的$F$的最优线性逼近, $x$逼近于$p$:$F_(x) \approx F_{(p)} + J_{F(p)} \cdot (x-p)$

从数学意义上来解释雅可比矩阵，我们可以想象有6个函数，每个函数对应着有6个变量。那么针对每个输入变量$x_i$，就会能够得到对应的$y_i$.
$$y_1=f_1(x_1,x_2,x_3,x_4,x_5,x_6)$$
$$y_2=f_2(x_1,x_2,x_3,x_4,x_5,x_6)$$
$$y_3=f_3(x_1,x_2,x_3,x_4,x_5,x_6)$$
$$y_4=f_4(x_1,x_2,x_3,x_4,x_5,x_6)$$
$$y_5=f_5(x_1,x_2,x_3,x_4,x_5,x_6)$$
$$y_6=f_6(x_1,x_2,x_3,x_4,x_5,x_6)$$
因此$y_i$的导数可以被写成：
$${\mathrm{d} y_i} = \frac{\partial f_i}{\partial x_1}{\mathrm{d} x_1}+\frac{\partial f_i}{\partial x_2}{\mathrm{d} x_2}+\frac{\partial f_i}{\partial x_3}{\mathrm{d} x_3}+\frac{\partial f_i}{\partial x_4}{\mathrm{d} x_4}+\frac{\partial f_i}{\partial x_5}{\mathrm{d} x_5}+\frac{\partial f_i}{\partial x_6}{\mathrm{d} x_6}$$
因此结合上面的方程，我们可以将上面的方程写为向量的形式：
$${\mathrm{d} Y}=\frac{\partial F}{\partial X}{\mathrm{d} X}$$
函数F对于X的偏导数矩阵，就被称为雅可比矩阵(Jacobian)。

换句话说，雅可比矩阵就是X的速度到Y的速度的映射：$\dot{Y}=J(X)\dot{X}$
在某个时间步长，雅可比矩阵其实也就是针对于$x_i$的函数。在下一个时间步长的时候，$x$改变了，因此雅可比矩阵也进行了改变。

在某个给定点的雅可比行列式提供了在接近该点时的表现的重要信息. 例如, 如果连续可微函数$F$在$p$点的雅可比行列式不是零, 那么它在该点附近具有反函数. 这称为反函数定理. 更进一步, 如果pp点的雅可比行列式是正数, 则$F$在$p$点的取向不变；如果是负数, 则FF的取向相反. 而从雅可比行列式的绝对值, 就可以知道函数$F$在$p$点的缩放因子；这就是为什么它出现在换元积分法中.

对于取向问题可以这么理解, 例如一个物体在平面上匀速运动, 如果施加一个正方向的力$F$, 即取向相同, 则加速运动, 类比于速度的导数加速度为正；如果施加一个反方向的力$F$, 即取向相反, 则减速运动, 类比于速度的导数加速度为负.

Jacobian矩阵和Hessian矩阵
使用雅可比矩阵(Jacobian)来结算IK
如何理解雅克比矩阵?—知乎
雅克比矩阵、海森矩阵与非线性最小二乘间的关系与在SFM和Pose Estimation中的应用
acobian矩阵和Hessian矩阵
动画研究 – 使用雅可比矩阵(Jacobian)来结算IK

海森矩阵（Hessian matrix）

海森矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵.

此函数如下：$$f(x_1,\cdots,x_n)$$

如果 f 所有的二阶导数都存在，那么 f 的海森矩阵即：$H(f)_{ij}(x)=D_iD_jf(x)$其中$x=(x_1,x_2,\cdots,x_n)$，即是：

$$H(f)=\begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} &\frac{\partial^2 f}{\partial x_1\partial x_2} &\cdots &\frac{\partial^2 f}{\partial x_1\partial x_n} \ \frac{\partial^2 f}{\partial x_2\partial x_1} &\frac{\partial^2 f}{\partial x_2^2} &\cdots &\frac{\partial^2 f}{\partial x_2\partial x_n} \ \vdots &\vdots &\ddots &\vdots \ \frac{\partial^2 f}{\partial x_n\partial x_1} &\frac{\partial^2 f}{\partial x_n\partial x_2} &\cdots &\frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}$$

(也有人把海森定义为以上矩阵的行列式)海森矩阵被应用于牛顿法解决的大规模优化问题.

海森矩阵在牛顿法中的应用

一般来说, 牛顿法主要应用在两个方面:

• 求方程的根
• 最优化

求根

并不是所有的方程都有求根公式, 或者求根公式很复杂, 导致求解困难. 利用牛顿法, 可以迭代求解.

原理是利用泰勒公式, 在$x_0$处展开, 且展开到一阶, 即$f(x)=f(x_0)+(x-x_0)f’(x_0)$

求解方程$f(x)=0$，即求解$f(x_0)+(x-x_0)f’(x_0) = 0$

即是求解$$x=x_1=x_0-\frac{f(x_0)}{f’(x_0)}$$

因为这是利用泰勒公式的一阶展开,$f(x)$的值是近似相等，这里求得的$x_1$，只能让$f(x_1) \approx 0$。于是乎, 迭代求解的想法就很自然了, 可以进而推出：$x_{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}$， 通过迭代, 这个式子必然在$f(x^*)=0$的时候收敛.过程如下图：

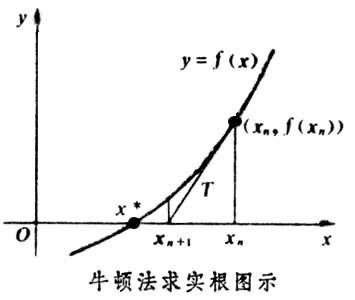
最优化

在最优化的问题中, 线性最优化至少可以使用单纯形法(或称**不动点算法**)求解, 但对于非线性优化问题, 牛顿法提供了一种求解的办法.假设任务是优化一个目标函数$f$,求函数$f$的极大极小问题可以转化为求解函数$f$的导数${f}’=0$的问题。, 这样求可以把优化问题看成方程(${f}’=0$)求解问题。剩下的问题就和前面提到的牛顿法求解很相似了。

这次为了求解${f}’=0$的根, 首先把$f(x)$在探索点$x_n$处泰勒展开, 展开到2阶形式进行近似：

$$f(x)=f(x_n)+f’(x_n)(x-x_n)+\frac{f’’(x_n)}{2}(x-x_n)^2$$

然后用$f(x)$的最小点做为新的探索点$f(x+1)$，据此，令：

$$f’(x)=f’(x_n)+f’’(x_n)(x-x_n)=0$$

求得出迭代公式:

$$x_{n+1}=x_n-\frac{f’(n)}{f’’(n)},n=0,1,…$$

一般认为牛顿法可以利用到曲线本身的信息, 比梯度下降法更容易收敛（迭代更少次数）, 如下图是一个最小化一个目标方程的例子, 红色曲线是利用牛顿法迭代求解, 绿色曲线是利用梯度下降法求解.

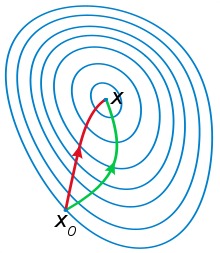
在上面讨论的是2维情况, 高维情况的牛顿迭代公式是：

$$x_{n+1}=x_n-[\bigtriangledown ^2f(x_n)]^{-1}\bigtriangledown f(x_n),n\geqslant 0$$

其中$\bigtriangledown ^2$是Hessian矩阵，$\bigtriangledown$为$f$的梯度向量，$f$的矢量微分运算。

高维情况依然可以用牛顿迭代求解, 但是问题是Hessian矩阵引入的复杂性, 使得牛顿迭代求解的难度大大增加, 但是已经有了解决这个问题的办法就是Quasi-Newton method, 不再直接计算Hessian矩阵, 而是每一步的时候使用梯度向量更新Hessian矩阵的近似.

Reference：
Jacobian矩阵和Hessian矩阵
雅克比矩阵、海森矩阵与非线性最小二乘间的关系与在SFM和Pose Estimation中的应用
最优化方法:牛顿迭代法和拟牛顿迭代法

最小二乘

最小二乘法的本质是最小化系数矩阵所张成的向量空间到观测向量的欧式误差距离.

最小二乘法的一种常见的描述是残差满足正态分布的最大似然估计

现行的最小二乘法是勒让德( A. M. Legendre)于1805年在其著作《计算慧星轨道的新方法》中提出的。它的主要思想就是选择未知参数，使得理论值与观测值之差的平方和达到最小：$H = \sum_{0}^{m}(y-y_i)^2$

##线性最小二乘问题

采用线性模型去拟合数据，即$y(x)=Jx$，则目标函数为$f(x)=\frac{1}{2}||Jx-y||^2$，同时$\bigtriangledown f(x)=J^T(Jx-y)$，

$\bigtriangledown^2 f(x)=J^TJ$。

根据最优化定理，该问题的最优解满足如下条件：$\bigtriangledown f(x)=0$，即是$J^TJx=J^Ty$。

求解该方程，有如下方法:

1. **Cholesky分解**：当m>>n时，并且J比较稀疏时比较实用，但是其精度和条件数的平方相关
2. **QR分解**：精度和条件数相关
3. **SVD分解**：相对比较鲁棒，同时也可以添加正则项避免J是个病态矩阵。
4. 数值迭代算法：对于大规模数据比较实用。

非线性最小二乘问题

采用非线性模型拟合数据，模型本身可能矢量梯度或者Hessian矩阵不容易得到。

高斯牛顿方法（Gauss-Newton方法）

根据标准牛顿方程，$\bigtriangledown f(x_k)p=-\bigtriangledown f(x_k) $可以得到该问题的需要满

足的条件，即$J^TJP^{GN}=-J^Tr_K$

此时Hessian矩阵用第一项代替，即$\bigtriangledown^2f(x) \approx J^TJ$

得到搜索方向后，可以使用线搜索的方法得到步长，重复进行可以得到最优解。

Reference:
最小二乘问题(Least-Squares)
最小二乘法 来龙去脉
最小二乘法的参数估计
一元线性回归模型与最小二乘法及其C++实现
机器视觉中的非线性最小二乘法
最小二乘法，牛顿法，梯度下降法以及比较
机器学习经典算法之—–最小二乘法