自动微分法

几种微分求解的方法

  • 手动求解法(Manual Differentiation)
  • 数值微分法(Numerical Differentiation)
  • 符号微分法(Symbolic Differentiation)
  • 自动微分法(Automatic Differentiation)

自动微分

在数学和计算代数领域，automatic differentiation (AD)又称为 algorithmic differentiation 或者 computational differentiation。AD是一个可以对程序代码表示的数学函数进行自动微分的技术。AD利用链式法则来达到自动求解的目录，AD有两种主要的方法：

  • 代码转换（source-code transformation）（R. Giering and T. Kaminski. 1998）：
    • 利用一个代码转换编译器，这个编译器会分析源代码，然后产生一个和源代码对应的伴随模式(adjoint model)程序，编译时的代码生成（如用 flex-bison 做词法、语法分析）；
    • 优点是静态生成效率高(原始算法的3~4倍) ;
    • 一次生成，多次使用，缺点是学习门槛较高（编译原理…）；
    • 很多比较好的工具非免费；
    • 对现代编程语言特性的限制（如C++类、模板等）；
  • 运算符重载(operator overloading)
    • 应用比较广泛，很多编程语言特性可以很好的工作；
    • 优点是简单直接，缺点是动态生成成本较高（代表性的工具效率是原始算法的10~35倍）。
    • 较多免费开源 C++ 工具 (e.g. ADOL-C, CppAD, Sacado)；

AD 这两种实现方式：运算符重载与代码生成，两种方式的原理都一样， 链式法则。AD相关工具，请到这个http://www.autodiff.org/ 页面。自动微分（AD）是计算导数的最优方法，比符号计算、有限微分更快更精确，AD已经广泛应用在优化领域，包括人工神经网络的训练算法 back-propagation（BP）等。

AD基本原理

链式法则

AD基本原理是链式法则。链式法则又分为正向和反向。如下例子

$$y=f(g(h(x)))=f(g(h(w_0)))=f(g(w_1))=f(w_2)=w_3$$

那么链式法则就表示为:

$$\frac{dy}{dx}=\frac{dy}{dw_2}\frac{dw_2}{dw_1}\frac{dw_1}{dx}$$

正向链式法则：则从链里往外算（即，先算$\frac{dw_1}{dx}$，再算$\frac{dw_2}{dw_1}$，最后算$\frac{dy}{dw_2}$）。

反向链式法则：则从链外往外里（即，先算$\frac{dy}{dw_2}$，再算$\frac{dw_2}{dw_1}$，最后算$\frac{dw_1}{dx}$）。

简洁的表示为：

正向链式法则：计算递归式$$\frac{dw_i}{dx}=\frac{dw_i}{dw_{i-1}}\frac{dw_{i-1}}{dx}，且w_3=y$$

反向链式法则：计算递归式$$\frac{dy}{dw_i}=\frac{dy}{dw_{i+1}}\frac{dw_{i+1}}{dw_i}，且w_0=y$$

通常，正向跟反向链式法则都是通过计算图来表示和计算，这样更加的方便。

正向链式法则计算图

将函数转化为一个DAG（有向无环图），就能很容易的求解每一步的值。

例1：

假设有计算式子：$y=x_0*x_1+x_1$ (1)，我们要求解$\frac{\partial y}{\partial x_1}$。

首先，其计算图表示为：

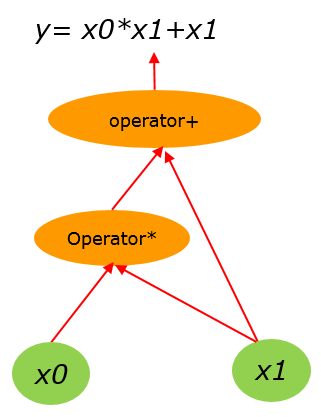
计算图1.png

把（1）式展开为链式计算序列为：

1
2
3
c=x0*x1
d=c+x1
y=d

那么其对应的计算图则为：

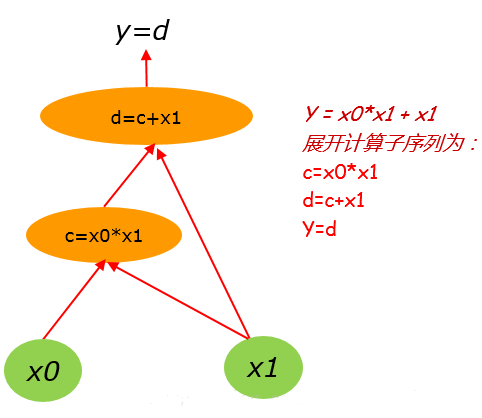
计算图2.png

这里假设$x_0,x_1$的初值分别为：1, 2。 (1)式展开计算子序列为：

1
2
3
4
5
x0=1
x1=2
c=x0*x1
d=c+x1
y=d

那么其对应计算图为：

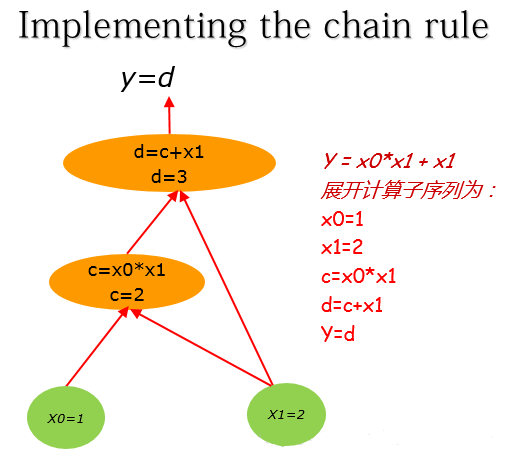
计算图3.png

然后对该计算图求解偏导数：

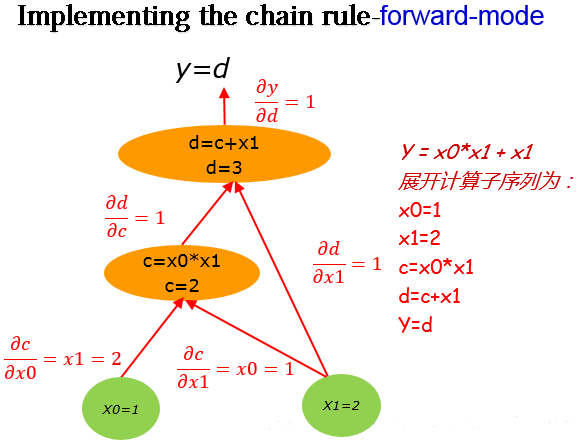
计算图4.png

由链式法则得到：$$\frac{\partial y}{\partial x_1}=\frac{\partial y}{\partial d}\frac{\partial d}{\partial c}\frac{\partial c}{\partial x_1}+\frac{\partial y}{\partial d}\frac{\partial d}{\partial x_1}$$

结合计算图中对应的值可知：$\frac{\partial y}{\partial x_1}=1\times1\times1+1\times1=2$

例2：

对于下列函数：$$f(x_1,x_2)=ln(x_1)+x_1*x_2-sin(x_2)$$

转化为计算图：

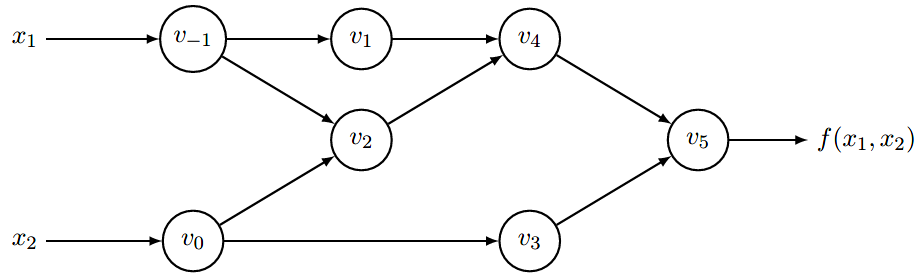
计算图5.png

那么求每一步的导数值就可以表示为：

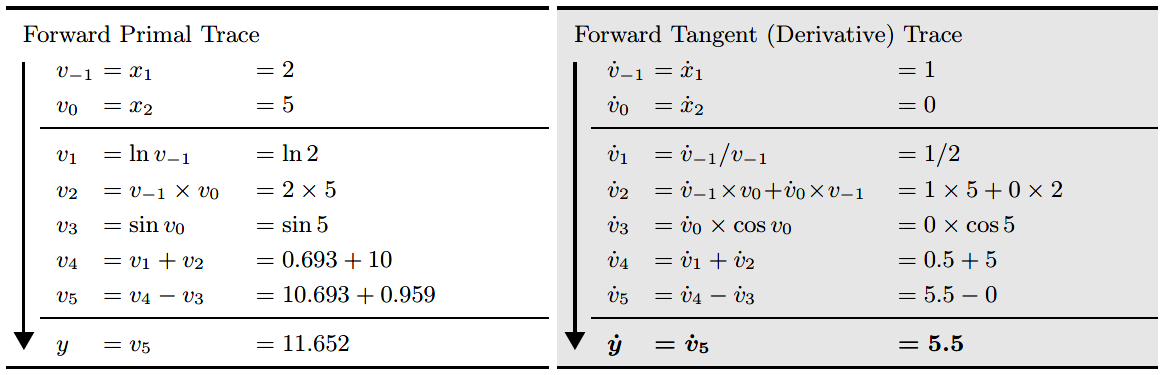
计算图6.png

上表，左半部分是从左往右计算图每个节点的求值结果，右半部分是每个节点对于$x_1$的求导结果，比如$\dot{v_1}=\frac{dv}{dx_1}$，注意到每一步的求导都会利用到上一步的求导结果。

对于自动微分的正向模式，如果函数输入输出为：$R \rightarrow R^m $

那么正向模式只需要计算一次上表右侧过程即可，非常高效。但是对于输入输出映射为：$R^n\rightarrow R^m$，这样一个有$n$个输入的函数，对于函数的梯度求解则需要处理$n$遍上述过程。而且再实际算法模型中，通常输入输出是极度不成比例的，也就是$n>>m$，那么利用正向模式进行自动微分的效率就太低了，因此有了反向模式的出现。

反向链式法则计算图

自动微分的反向模式其实就是一种通用的BackPropagation(反向传播算法)，即backpropagation是自动微分反向模式的一种特殊形式。

反向模式从最终结果开始求导，利用最终输出对每一个节点进行求导，其过程如下计算图所示：

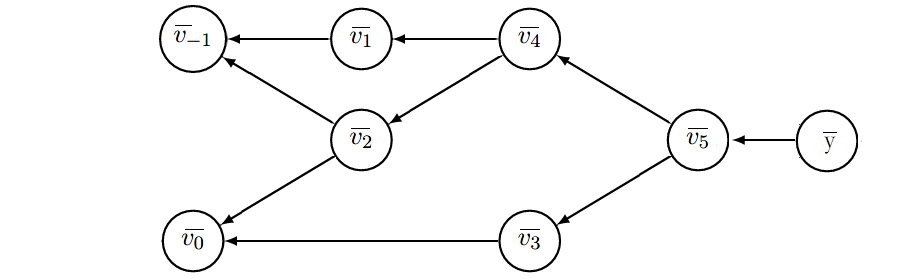
计算图7.png

其具体计算过程如下表所示：

计算图8.png

上表左边和之前的正向模式一致，用于求解函数值，右边则是反向模式的计算过程，须从下向上看，也就是一开始先计算输出$y$对于节点$v_5$的导数，用$\bar{v_5}=\frac{dy}{dv_5}$，这样的记号可以强调我们对当前计算结果进行缓存，以便用于后续计算，而不必重复计算。再由链式法则我们可以计算输出节点对于图种每个节点的导数。

比如对节点$v_3$：

$$\frac{y}{v_3}=\frac{dy}{dv_5}\frac{dv_5}{dv_3}$$

用$\bar{v_i}=\frac{dy}{dv_i}$记法，则有：

$$\frac{y}{v_3}=\bar{v_5}\frac{dv_5}{dv_3}$$

比如对于节点$v_0$：

$$\frac{y}{v_0}=\frac{dy}{dv_2}\frac{dv_2}{dv_0}+\frac{dy}{dv_3}\frac{dv_3}{dv_0}$$

用$\bar{v_i}=\frac{dy}{dv_i}$记法，则有：

$$\frac{y}{v_0}=\bar{v_2}\frac{dv_2}{dv_0}+\bar{v_3}\frac{dv_3}{dv_0}$$

和backpropagation算法一样，我们必须记住前向时当前节点发出的边，然后在反向传播时，可以搜集所有受到当前节点影响的节点。

如上的计算过程，对于像神经网络这种模型，输入通常是上万到上百万维，而输出损失函数是1维的模型，则只需要一遍反向模式计算过程，便可以求出输出对于各个输入的导数，从而轻松求取梯度用于后续优化更新。

参考

AD:

BP: